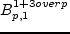
Le but de l'exposé est de présenter un résultat d'existence et d'unicité globale pour le système d'Euler axisymétrique pour des données initiales dans les espaces de Besov critiques avec p dans [1,+\infty]. Dans ce cas, le critère de BKM n'est pas valable et pour contourner cette difficulté, nous utilisons une nouvelle décomposition de la vorticité. Il s'agit d'une amélioration d'un résultat que nous avons obtenu en 2007. Ceci donne une réponse définitive à une question soulevée par R. Danchin dans un article récent.

L'équation de Gross-Pitaevskii offre une grande richesse de régimes et de solutions spéciales. Je discuterai tout d'abord de l'existence d' ondes progressives en dimensions 1,2 et 3 d'espace , ainsi que de leurs propriétés : stabilité orbitale, limit transsonique vers l'équation de KP, etc...Cette partie est basée sur des travaux avec Jean-Claude Saut, Philippe Gravejat et Didier Smets. Dans un deuxième temps, je discuterai d'un autre régime, qui correspond d'une certaine manière à une limite "onde longue" (cette partie est basée sur des travaux en cours avec Raphaël Danchin et Didier Smets).

Nous considérons les équations de Kadomtsev-Petviashvili-Burgers et (KPB I et II). Plus particulièrement, nous établissons des résultats d'existence pour les équations de KPB I et II autour d'ondes progressives monotones de l'équation de KdV-Burgers. Nous montrons que les ondes progressives monotones de KdV-Burgers sont stables et asymptotiquement stables sous la dynamique de KPB I par rapport à des petites perturbations dans l'espace d'énergie.

Le système de Born-Infeld (abrégé systéme BI) est une version non linéaire des équations de Maxwell classiques. Il a été introduit par M. Born et L. Infeld dans les années 30 pour décrire un phénomène physique de l'électromagnétisme. Récemment, le système de Born-Infeld a attiré l'attention en raison de ces nouvelles applications dans la théorie des cordes et de la physique des hautes énergies.

Nous allons considérer le cas où les équations BI dépendent d'un paramètre pouvant être interprété comme un champ électrique maximal dans la théorie de l'électromagnétisme et le cas correspondant à la théorie des cordes.

Dans cet exposé, nous augmenterons le système BI dépendant de pour obtenir un système augmenté (appelé système ABI) de la même façon que Y. Brenier. Nous montrerons la structure hyperbolique du système ABI pour tout , ce qui entraîne l'existence d'une solution entropique globale dans . Ces résultats sont l'extension des résultats correspondant à . Nous donnerons en particulier une expression explicite de la solution entropique.

Ensuite, nous considèrerons les limites formelles quand et . Nous obtiendrons respectivement les équations de Maxwell et les équation de la magnétohydrodynamique sans pression (pour la limite , un changement d'échelle sera introduit). Finalement, en utilisant des arguments de compacité par compensation, nous justifierons rigoureusement la limite pour des solutions entropiques en une dimension.

On s'intéresse à l'existence ou à la stabilité de solutions faibles pour différents modèles magnétiques de fluides compressibles visqueux. Les choix des profils de viscosité et de résistivité des fluides sont le point central de ces études puisqu'ils conditionnent les résultats enoncés dans cet exposé. En particulier on proposera une généralisation magnétique d'un résultat de Feireisl et al. sur Navier-Stokes compressible adiabatique pour des viscosités constantes et on verra d'autre part comment la récente étude de Bresch et Desjardins sur le modèle Navier-Stokes complet avec température et viscosités dépendantes de la densité est un bon outil pour l'étude de certains modèles magnétiques à un ou deux fluides avec viscosités et résistivité variables.